DEGUCHI LABORATORY
Department of Physics, Ochanomizu University
Japanese/English

可積分量子多体系の非平衡ダイナミクス


研究背景-孤立量子多体系の緩和-


最近、冷却原子系の実験研究が発展する中で、孤立した一次元ボース気体の時間発展が観測され、ボース粒子の集団が振動するという興味深い現象[K] が観察された。この実験を一つの契機として、孤立量子系の時間発展に関心が集まり、非可積分量子系や可積分量子系の純粋状態の時間発展が多くの研究者によって調べられている。

非可積分量子系の場合、孤立系の純粋状態の時間発展でエントロピーは変化しないにもかかわらず、局所的な物理量の状態期待値はミクロカノニカル分布による熱平衡値に漸近することが、シミュレーション等で調べられ、定性的な議論でも示唆されている。従来の常識では、散逸のない孤立量子系が平衡状態へ漸近することは期待できない。一方、量子状態の典型性(typicality)および固有状態熱化の仮説(eigenstate thermalization hypotheis, ETH) の視点に立つと、孤立系であっても時間発展で熱化あるいは平衡化が示唆される。実際、Lebowitz 達によって、von Neumann の量子エルゴ―ド性に関する定理(1929) が最近再発見された。こうして今では、量子状態の典型性の考え方はvon Neumannに遡ると言える。しかし、一般の量子多体系の高精度かつ長時間のシミュレーションの実行は容易でなく、研究状況は研究開始当初はもとより、現在でも未だに混沌としていると言えるであろう。

さらに、可積分量子系の孤立系の場合には、平衡化によって一般化されたギブス分布(generalized Gibbs ensemble, GGE)に漸近する[R]、という興味深い仮説が提案された。可積分量子系では特別な初期状態を選べば、時間発展を長時間にわたって追跡することができる。そこで、多くの研究者がＧＧＥ仮説の検証に挑戦している。いくつかの可積分量子系に対して、様々な初期状態で時間発展が調べられた。その結果、現在ではＧＧＥの仮説に対する反例も知られている。


緩和や再帰性など量子ダイナミクスの特徴の解明


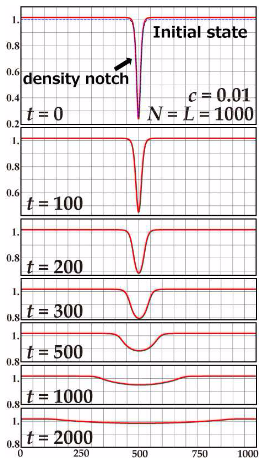
可積分量子多体系の時間発展を物理量演算子の期待値を数値的に計算して調べ、緩和現象や再帰的振る舞いの様子を明らかにした。さらに非可積分量子スピン系のシミュレーションと比較して、観察された量子ダイナミクスの特徴的振る舞いが普遍的かどうかを明らかにした。

δ関数型相互作用ボース気体の孤立局在波解の特徴づけ [2, 7, 8, 10, 11]

斥力のデルタ関数型相互作用をもつ１次元ボース気体において、ホール励起を重ね合わせると、密度プロファイルは空間的に一様でなく、密度の値が急激に減少する局在領域を持つ量子状態が導かれることが、本研究と密接に関係する共同研究の中で明らかにされた。その密度プロファイルはあたかもＧＰ方程式のダークソリトン解の振幅と同じような形であった[8]。この発見を定式化し、一般化を試みた。 斥力δ関数型相互作用の１次元ボース気体（Lieb-Liniger 模型）において、弱結合領域では、量子状態は古典的に振る舞い、Gross-Pitaevskii方程式（非線形シュレーディンガ―方程式）で記述されることが明らかになった[11]。すなわち、形状因子公式を用いてこの局在量子状態の密度プロファイルを求めたところ、１ソリトン解の振幅のプロファイルとほぼ完全に一致した。ただし、周期的境界条件のためソリトン解は楕円関数解である。また、ホール励起解の重ね合わせの量子状態に関して、Ｎ粒子の状態とＮ－１粒子の状態を求め、この二つの状態に関する量子場の演算子の行列要素を求めたところ、その振幅と位相は１ソリトン解のものに非常に良く一致することが分かった[11]。

量子ＸＸＸ鎖の局所磁化の形状因子公式はKitanine et al. (1999) で導かれていたが、数値的に安定でなかった。Slavnov の行列式からCauchy 行列式を分離し、漸近的にフレッドホルム行列式に収束する行列式の形にこの形状因子公式を改良した。スピノン状態の和で与えられる量子状態に対して、局所磁化の時間発展を求めた。


再帰時間の数値的評価


可積分量子系の励起エネルギーを求めて再帰時間を数値的に推測し、時間発展の結果と比較する。具体的には、斥力のデルタ関数型ポテンシャルで相互作用する１次元ボース気体の様々な量子状態に関して、時間発展した状態と初期状態の相関（フィデリティー）を数値的に調べて、再帰時間を求めた。


近藤模型や可積分高次スピンＸＸＺ鎖の量子ダイナミクス


磁性不純物の厳密解である近藤模型の時間相関関数の解析的表示を導き、不純物スピンの量子ダイナミクスの特徴を解明する。さらに、可積分高次スピンＸＸＺ鎖の絶対零度における時間相関関数の解析的表現を導く。後者は前者の拡張模型に相当し、不純物スピンの大きさが異なる近藤模型の厳密解などが導かれる。磁性不純物スピンのダイナミクスを明らかにした。

近藤問題など不純物を含む可積分量子系の解として、不純物サイトを持つ量子ＸＸＺ鎖の厳密解を導いた[6]。ＸＸＺ鎖中の不純物は１次元ラッティンジャー流体中の不純物に対応し、普遍性クラスはラッティンジャー流体パラメターで表されると予想される。基底状態に対するベーテ仮説方程式を解き、ウィーナーホップ法を積分範囲が非対称な場合に拡張し、絶対零度での不純物磁化率の解析的表式を求めた。そして低温での不純物比熱を熱力学的ベーテ仮説方程式の数値解から求めた。普遍性クラスを表すウィルソン比の解析的表式が導かれ、共形場理論の予想と一致した。ＸＸＺ鎖のdressed chargeつまり共形場のコンパクト化半径で表される。さらに代数的ベーテ仮説を用いて局所磁化演算子の期待値を直接計算し、有限磁場下での不純物磁化の解析的表式を導いた。従来の近藤問題の厳密解では、ベーテ仮説方程式に基づく物理的な議論で不純物磁化を導出していたが、上で求めた従来の方法での結果と一致した。代数的ベーテ仮説で従来の方法の正当性が裏付けられた[6]。


量子ＸＸＸ鎖のベーテ仮説方程式の解の探索


１次元量子ハイゼンベルグ模型（量子ＸＸＸ鎖）において、任意に与えられた量子状態を初期時刻の量子状態として出発する時間発展を追跡するためには、与えられた初期量子状態をベーテ固有状態の重ね合わせとして表すことができれば良い。そのためには、有限サイズの鎖上に定義された量子ＸＸＸ鎖のすべてのベーテ固有状態を求めることが重要である。このため、複素束縛解（ストリング解）も含めて有限サイズ系のベーテ仮説方程式の全ての解を数値的に求めることが、重要な技術的な課題の一つである。

格子点数１２の場合にＸＸＸ鎖のベーテ仮説方程式の解を全て求めた。特に解に対応するベーテ量子数を全て求めた[1]。局所磁化の形状因子の改良公式にこの数値解を代入すると、複素数値束縛解など任意のベーテ固有状態の重ね合わせで表されるどのような量子状態に対しても、物理量演算子の状態期待値の時間発展を導くことができる。

格子点数１２の有限サイズの系であっても、ベーテ仮説方程式の解とそれらに対応するベーテ量子数が全て求められたことは、今後、さらに大きなサイズの系に対してベーテ仮説方程式の数値解を求める上で指針となり、非常に役立つであろう。



※[10] と[11]は未出版。